UTILIZAS FUNCIONES POLINOMIALES DE GRADOS TRES Y CUATRO

Un modelo matemático se define como una descripcion desde el punto de vista de las matemáticas de un hecho o fenómeno del mundo real, desde el tamaño de la población, hasta fenómenos físicos como la velocidad, aceleración o densidad. El objetivo del modelo matemático es entender ampliamente el fenómeno y tal vez predecir su comportamiento en el futuro.

Modelos Lineales

Se dice que una función es lineal cuando su gráfica es una línea recta; y por consecuencia tiene la forma:
y = f(x) = mx + b
Donde m representa la pendiente de la recta y b la ordenada al origen (el punto en el que la recta interfecta al eje de las "y"). Es importante mencionar que este tipo de funciones crecen a tasa constante; y su dominio e imagen son todos los números reales.

Polinomios

Una función es polinomio si tiene la forma:
P(x) = anxn + an-1xn-1 + …… a2x2 + a1x + a0
Donde n representa un entero negativo y los números a0, a1, a2,….. an, son constantes llamadas coeficientes del polinomio. El dominio de todos los polinomios son todos los números reales (-∞, ∞).
Los polinomios se nombran de acuerdo al grado del primer termino. Los polinomios de grado uno son de la forma: P(x) = mx + b, y son funciones lineales. Los polinomios de segundo grado son llamados funciones cuadráticas y presentan la forma P(x) = axx + bx + c; su gráfica es de una parábola.
Una función de tercer grado, es llamada función cúbica, y tiene la forma: P(x) = ax3 + bx2 + cx + d. A continuación se muestran las gráficas de algunas funciones de polinomios.

Funciones potencia

Una función es llamada potencia, cuando tiene la forma: f(x) = xa, donde a es constante. Y hay varios casos:

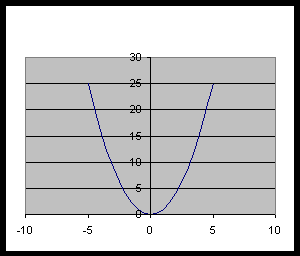
La forma genera de la gráfica depende si n es par o impar; si n es par, la gráfica de f es similar a la parábola y = x2; de lo contrario, la gráfica se parecerá a la función y = x3.
Es importante mencionar, que en cualquiera que sea el caso, cuando n crece, la gráfica se vuelve más plana cerca de 0, y más empinada cuando Ix I es menor o igual a 1.

La función f(x) = x1/n es una función raíz. Al igual que en el caso anterior, su gráfica depende de n, ya que si n es par su gráfica será similar al de raíz cuadrada; y si n es impar su gráfica será similar al de raíz cúbica.

Éste tipo de función es llamada función recíproca, y su forma es f(x) = x -1 o f(x) = -1/x. Y su gráfica corresponde a una hipérbola cuyas asíntotas son los ejes de coordenadas.