El dominio de una relación es el conjunto de preimágenes; es decir, el conjunto formado por los elementos del conjunto de partida que están relacionados. Al conjunto de imágenes, esto es, elementos del conjunto de llegada que están relacionados, se le denomina recorrido o rango.
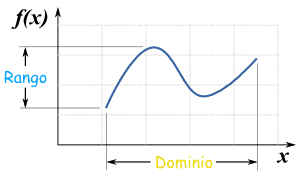En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.
Hay nombres especiales para lo que puede entrar, y también lo que puede salir de una función:
  |
Lo que puede entrar en una función se llama el dominio |
|
Lo que es posible que salga de una función se llama el codominio |
|
Lo que en realidad sale de una función se llama rango o imagen |
Entonces, en el diagrama de arriba el conjunto "X" es el dominio, el conjunto "Y" es el codominio, y los elementos de Y a los que llegan flechas (los valores producidos realmente por la función) son el rango.
Parte de la función
Lo que sale (el rango) depende de lo que pones (el dominio), pero NOSOTROS definimos el dominio.
De hecho el dominio es una parte esencial de la función. Un dominio diferente da una función diferente.
Ejemplo: una simple función como f(x) = x2 puede tener dominio (lo que entra) los números de contar {1,2,3,...}, y el rango será entonces el conjunto {1,4,9,...}
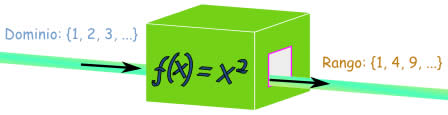
Y otra función g(x) = x2 puede tener como dominio los enteros {...,-3,-2,-1,0,1,2,3,...}, entonces el rango será el conjunto {0,1,4,9,...}
