EMPLEAS FUNCIONES POLINOMIALES DE GRADOS CERO, UNO Y DOS
¿Qué es una función polinomial?
Esto depende de los grados de la función. La función polinomial tiene relación con la expresión polinomial o con el polinomio. Si una expresión tiene muchos términos la función polinomial puede tenerlos o no, pero responde a la forma:
P(x)= anxn+an-1xn-1+an-2xn-2+…. + a0x0
Con la nota específica de que N es un nuero real y el coeficiente A no debe ser cero.
La función afín: FUNCIÓN POLINÓMICA DE GRADO 1 que tiene en su variable equis el exponente uno.
La forma de esta función de grado uno es la ecuación de la línea recta, que tiene su gráfica como aparece de forma oblicua.
y = m x + b



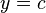



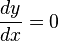
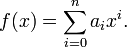
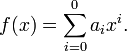

 La función identidad es la función: f(x)=x Es una función biyectiva
La función identidad es la función: f(x)=x Es una función biyectiva
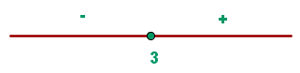
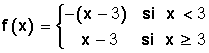
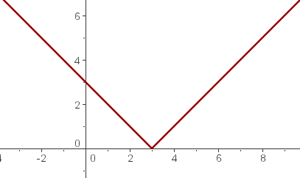 ESTOS SON UNOS EJEMPLOS ESPERO LES SIRVA DE GUIA :DD SUERTE
ESTOS SON UNOS EJEMPLOS ESPERO LES SIRVA DE GUIA :DD SUERTE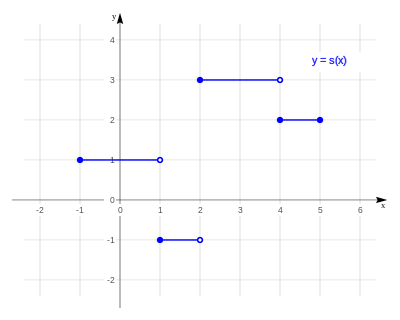
![\begin{array}{rrcl}
s : & [-1,5 ] \in R & \to & R \\
& x & \to & y = s(x)
\end{array}](https://upload.wikimedia.org/math/a/e/7/ae7b5307d50533629a546e36fe7055fc.png)

 , se llama función inversa de
, se llama función inversa de  y se denota por
y se denota por  a otra función que para cualquier valor del dominio de
a otra función que para cualquier valor del dominio de 
 , proviene de un único valor del dominio
, proviene de un único valor del dominio  .
.
 e
e  .
. .
. y después despejamos la
y después despejamos la 
 es
es  .
.


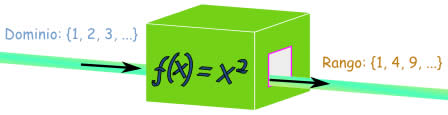
 En cuanto a la diferencia entre imagen y contradominio (o codominio) de una función es lo siguiente: se denomina contradominio de una función LO QUE ES POSIBLE QUE SALGA de la función; se denomina imagen de una función LO QUE EN REALIDAD SALE de la función. Ejemplo:
En cuanto a la diferencia entre imagen y contradominio (o codominio) de una función es lo siguiente: se denomina contradominio de una función LO QUE ES POSIBLE QUE SALGA de la función; se denomina imagen de una función LO QUE EN REALIDAD SALE de la función. Ejemplo: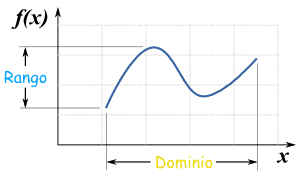 En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.
En su forma más simple el dominio son todos los valores a los que aplicar una función, y el rango son los valores que resultan.