https://www.youtube.com/watch?v=genKpxlUGT8 otro tutorial mas q espero sea de ayuda jeje

https://www.youtube.com/watch?v=nJol6Qatm-s

este es un tutorial espero les sirva

AQUI LES EXPLICARE UN POCO E INCLUSO LES DEJO UN PEQUEÑO PROBLEMITA QUE NOS PUSIERON EN LA ESCUELA MMMM ESPERO LE ENTIENDAN JAJA:

Para identificar las aplicaciones una función polinomial de grado tres, presentamos una situación común de construcción.

Se tiene una hoja cuadrada de cartón de72 cm de lado y quieres construir una caja para sus cosas recortando un cuadrado de cada esquina. ¿Cuáles deben ser las dimensiones del cuadrado recortado para que el volumen de la caja sea el máximo?

En esta situación se dispone de la lámina completa en la que se puede recortar un cuadrado de lado “x”. al cortar cada esquina y doblar las partes restantes para obtener la caja de base cuadrada cuyas dimensiones son, en la base, 72 – 2x centímetros de lado y una altura de x centímetros.

El volumen de cualquier caja se obtiene como el producto de cada una de sus aristas, para este caso:

V= (72-2x)² x y desarrollando y simplificando se obtiene:

V = 4x³ – 288x² + 5 184x

Esta expresión algebraica determina el volumen máximo, pero necesitamos saber cuánto hay que recortar para que así sea. Pero si encontramos las raíces de esta función obtenernos el valor para que sea cero la función y no el valor de x para un mayor volumen. Al realizar un tabla de valores para x y y, encontraremos que hay un máximo volumen en 12 centímetros.

Propiedades Algebraicas y Geométricas de las Funciones Cuadráticas de Segundo Grado ó Parabólicas
Se llama función cuadrática a aquella cuya expresión algebraica en una sola variable es de gado dos. Y se les dice parabólicas o de parábola, porque su gráfica es una parábola.

Donde:
y es la variable dependiente
x la variable independiente
a.x2 es el término cuadrático
a es el coeficiente cuadrático
b.x es el término lineal
b es el coeficiente lineal
c es el término independiente
 
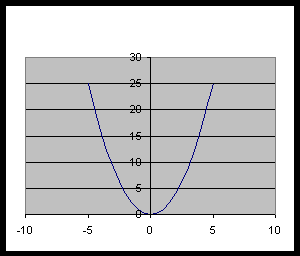
Dado que el cuadrado de números opuestos es siempre positivo, la gráfica de esta función es una parábola, cuyas ramas estarán para el lado positivo del eje de las ordenadas si a es positivo, caso contrario si a es negativo.-
O sea que:
Función positiva: las ramas de la parábola hacia la parte positiva del eje de las ordenadas (arriba)
Función negativa: las ramas de la parábola hacia la parte negativa del eje de las ordenadas (abajo)

UTILIZAS FUNCIONES POLINOMIALES DE GRADOS TRES Y CUATRO

Un modelo matemático se define como una descripcion desde el punto de vista de las matemáticas de un hecho o fenómeno del mundo real, desde el tamaño de la población, hasta fenómenos físicos como la velocidad, aceleración o densidad. El objetivo del modelo matemático es entender ampliamente el fenómeno y tal vez predecir su comportamiento en el futuro.

Modelos Lineales

Se dice que una función es lineal cuando su gráfica es una línea recta; y por consecuencia tiene la forma:
y = f(x) = mx + b
Donde m representa la pendiente de la recta y b la ordenada al origen (el punto en el que la recta interfecta al eje de las "y"). Es importante mencionar que este tipo de funciones crecen a tasa constante; y su dominio e imagen son todos los números reales.

Polinomios

Una función es polinomio si tiene la forma:
P(x) = anxn + an-1xn-1 + …… a2x2 + a1x + a0
Donde n representa un entero negativo y los números a0, a1, a2,….. an, son constantes llamadas coeficientes del polinomio. El dominio de todos los polinomios son todos los números reales (-∞, ∞).
Los polinomios se nombran de acuerdo al grado del primer termino. Los polinomios de grado uno son de la forma: P(x) = mx + b, y son funciones lineales. Los polinomios de segundo grado son llamados funciones cuadráticas y presentan la forma P(x) = axx + bx + c; su gráfica es de una parábola.
Una función de tercer grado, es llamada función cúbica, y tiene la forma: P(x) = ax3 + bx2 + cx + d. A continuación se muestran las gráficas de algunas funciones de polinomios.

Funciones potencia

Una función es llamada potencia, cuando tiene la forma: f(x) = xa, donde a es constante. Y hay varios casos:

La forma genera de la gráfica depende si n es par o impar; si n es par, la gráfica de f es similar a la parábola y = x2; de lo contrario, la gráfica se parecerá a la función y = x3.
Es importante mencionar, que en cualquiera que sea el caso, cuando n crece, la gráfica se vuelve más plana cerca de 0, y más empinada cuando Ix I es menor o igual a 1.

La función f(x) = x1/n es una función raíz. Al igual que en el caso anterior, su gráfica depende de n, ya que si n es par su gráfica será similar al de raíz cuadrada; y si n es impar su gráfica será similar al de raíz cúbica.

Éste tipo de función es llamada función recíproca, y su forma es f(x) = x -1 o f(x) = -1/x. Y su gráfica corresponde a una hipérbola cuyas asíntotas son los ejes de coordenadas.

Parámetros

Los parámetros se usan para mandar valores a las funciones. Una función trabajará con los parámetros para realizar las acciones. Por decirlo de otra manera, los parámetros son los valores de entrada que recibe una función.

Múltiples parámetros

Una función puede recibir tantos parámetros como queramos y para expresarlo se colocan los nombres de los parámetros separados por comas, dentro de los paréntesis.

Los parámetros se pasan por valor

Al hilo del uso de parámetros en nuestros programas Javascript, tenemos que saber que los parámetros de las funciones se pasan por valor. Esto quiere decir que estamos pasando valores y no variables.

Se usan para mandar valores a la función, con los que ella
trabajará para realizar las acciones. Son los valores de entrada que recibe una
función. Por ejemplo, una función que realizase una suma de dos números tendría
como parámetros a esos dos números. Los dos números son la entrada, así como la
salida sería el resultado, pero eso lo veremos más tarde.

• las de grado cero son rectas horizontales

• las de grado uno son rectas oblicuas

• las de grado dos son parábolas cuyo eje es paralelo al de ordenadas

Se trata de funciones continuas cuyo dominio es el conjunto de los números reales.

En matemáticas, la gráfica de una función:

7 la representación gráfica de la correspondencia entre los elementos del conjunto dominio y los del conjunto imagen. Es el conjunto formado por todos los pares ordenados (x, f(x)) de la función f; es decir, como un subconjunto del producto cartesiano X×Y.

Las únicas funciones que se pueden trazar de forma completa son las de una sola variable, con un sistema de coordenadas cartesianas, donde cada abscisa representa un valor de la variable del dominio y cada ordenada representa el valor correspondiente del conjunto imagen. Si la función es continua, entonces la gráfica formará una línea recta o curva.

En el caso de funciones de dos variables es posible visualizarlas de forma unívoca mediante una proyección geométrica, pero a partir de tres variables tan solo es posible visualizar cortes (con un plano) de la función para los que los valores de todas las variables, excepto dos, permanezcan constantes.

El concepto de gráfica de una función se generaliza a la gráfica de una relación. Notar que si bien cada función tiene una única representación gráfica, pueden existir varias funciones que tengan la misma, pero con dominios y codominios diferentes.

REPRESENTACION DE FUNCION GRADO 0.

REPRESENTACION DE UNA FUNCION GRADO UNO.

REPRESENTACION DE UNA FUNCION DE GRADO DOS.

FUNCIÓN POLINÓMICA DE GRADO 0

y = k

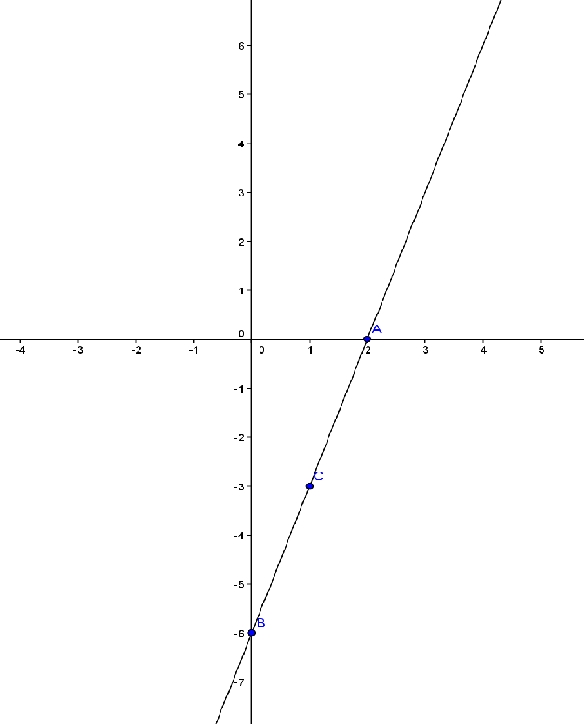
La función afin: FUNCIÓN POLINÓMICA DE GRADO 1

Se denomina función afin a toda función de la forma:

y = m * x + k

donde m (distinto de 0) y k son números reales.

La función cuadrática:

FUNCIÓN POLINÓMICA DE GRADO 2

Se denomina función cuadrática a toda función de la forma:

y=a*x²+b*x+c

donde a (distinto de 0), b y c son números reales.

NOTA: CUALQUIER FUNCION CUADRATICA ES PARABOLA :DD

SU DEFINICION PUEDE SER:

Las funciones polinomiales están entre las expresiones mas sencillas del álgebra. Es fácil evaluarlas, solo requieren sumas multiplicaciones repetidas. Debido a esto, con frecuencia se usan para aproximar otras funciones mas complicadas. Una función polinomial es una función cuya regla esta dada por un polinomio en una variable. El grado de una función polinomial es el grado del polinomio en una variable, es decir, la potencia mas alta que aparece de x.

Función Lineal

Una función lineal es una función polinomial de grado 1.

Función Cuadratica

Si el grado de una función polinomial es 2, se llama Función Cuadrática.

Una funcion es un conjunto de parejas ordenadas, en donde no hay dos parejas con el mismo primer elemento.

el conjunto de el primer elemento de las parejas se les llama dominio y al segundo conjunto de la primer pareja se les llama contradominio, para establecer la asociacion entre los elementos del dominio  con los elementos del contradominio se emplea una regla de correspondencia.

Las funciones se clasifican de acuerdo a las reglas de correspondencia como funciones algebraicas. (polinomicas, racionales y no radicales)

exponenciales, logaritmicas y trigonometricas en este espacio solo se trataran las funciones polinomiales.

existen tres formas de expresar el comportamiento de una funcion: una tabla que muestra al conjunto de parejas, la formula o exprecion algebraica, de la regla de correspondencia y la grafica de la funcion.

la grafica de una funcion nos sirve de mucha ayuda para observar como se comporta dentro de su dominio o algun intervalo de valores de este, emplearemos el sistema de coordenadas rectangulares para elaborar la grafica de la funcion.

para realizar la grafica de una funcion, primero se debe determinar cual es su dominio.