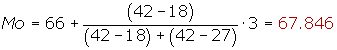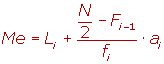Indica que variables son cualitativas y cuales cuantitativas:
1Comida Favorita.
2Profesión que te gusta.
3Número de goles marcados por tu equipo favorito en la última temporada.
4Número de alumnos de tu Instituto.
5El color de los ojos de tus compañeros de clase.
6Coeficiente intelectual de tus compañeros de clase.
2De las siguientes variables indica cuáles son discretas y cuales continuas.
1Número de acciones vendidas cada día en la Bolsa.
2Temperaturas registradas cada hora en un observatorio.
3Período de duración de un automóvil.
4El diámetro de las ruedas de varios coches.
5Número de hijos de 50 familias.
6Censo anual de los españoles.
3Clasificar las siguientes variables en cualitativas y cuantitativas discretas o continuas.
1La nacionalidad de una persona.
2Número de litros de agua contenidos en un depósito.
3Número de libros en un estante de librería.
4Suma de puntos tenidos en el lanzamiento de un par de dados.
5La profesión de una persona.
6El área de las distintas baldosas de un edificio.
4Las puntuaciones obtenidas por un grupo en una prueba han sido:
15, 20, 15, 18, 22, 13, 13, 16, 15, 19, 18, 15, 16, 20, 16, 15, 18, 16, 14, 13.
Construir la tabla de distribución de frecuencias y dibuja el polígono de frecuencias.
5El número de estrellas de los hoteles de una ciudad viene dado por la siguiente serie:
3, 3, 4, 3, 4, 3, 1, 3, 4, 3, 3, 3, 2, 1, 3, 3, 3, 2, 3, 2, 2, 3, 3, 3, 2, 2, 2, 2, 2, 3, 2, 1, 1, 1, 2, 2, 4, 1.
Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
6Las calificaciones de 50 alumnos en Matemáticas han sido las siguientes:
5, 2, 4, 9, 7, 4, 5, 6, 5, 7, 7, 5, 5, 2, 10, 5, 6, 5, 4, 5, 8, 8, 4, 0, 8, 4, 8, 6, 6, 3, 6, 7, 6, 6, 7, 6, 7, 3, 5, 6, 9, 6, 1, 4, 6, 3, 5, 5, 6, 7.
Construir la tabla de distribución de frecuencias y dibuja el diagrama de barras.
7Los pesos de los 65 empleados de una fábrica vienen dados por la siguiente tabla:
| Peso | [50, 60) | [60, 70) | [70, 80) | [80,90) | [90, 100) | [100, 110) | [110, 120) |
| fi | 8 | 10 | 16 | 14 | 10 | 5 | 2 |
1Construir la tabla de frecuencias.
2Representar el histograma y el polígono de frecuencias.
8Los 40 alumnos de una clase han obtenido las siguientes puntuaciones, sobre 50, en un examen de Física.
3, 15, 24, 28, 33, 35, 38, 42, 23, 38, 36, 34, 29, 25, 17, 7, 34, 36, 39, 44, 31, 26, 20, 11, 13, 22, 27, 47, 39, 37, 34, 32, 35, 28, 38, 41, 48, 15, 32, 13.
1Construir la tabla de frecuencias.
2Dibujar el histograma y el polígono de frecuencias.
9Sea una distribución estadística que viene dada por la siguiente tabla:
| xi | 61 | 64 | 67 | 70 | 73 |
| fi | 5 | 18 | 42 | 27 | 8 |
Calcular:
1La moda, mediana y media.
2El rango, desviación media, varianza y desviación típica.
10Calcular la media, la mediana y la moda de la siguiente serie de números: 5, 3, 6, 5, 4, 5, 2, 8, 6, 5, 4, 8, 3, 4, 5, 4, 8, 2, 5, 4.
11Hallar la varianza y la desviación típica de la siguiente serie de datos:
12, 6, 7, 3, 15, 10, 18, 5.
12Hallar la media, mediana y moda de la siguiente serie de números:
3, 5, 2, 6, 5, 9, 5, 2, 8, 6.
13Hallar la desviación media, la varianza y la desviación típica de la series de números siguientes:
2, 3, 6, 8, 11.
12, 6, 7, 3, 15, 10, 18, 5.
14Se ha aplicado un test a los empleados de una fábrica, obteniéndose la siguiente tabla:
| fi | |
| [38, 44) | 7 |
| [44, 50) | 8 |
| [50, 56) | 15 |
| [56, 62) | 25 |
| [62, 68) | 18 |
| [68, 74) | 9 |
| [74, 80) | 6 |
Dibujar el histograma y el polígono de frecuencias acumuladas.
15Dadas las series estadísticas:
3, 5, 2, 7, 6, 4, 9.
3, 5, 2, 7, 6, 4, 9, 1.
Calcular:
1La moda, la mediana y la media.
2La desviación media, la varianza y la desviación típica.
3Los cuartiles 1º y 3º.
4Los deciles 2º y 7º.
5Los percentiles 32 y 85.
16Una distribución estadística viene dada por la siguiente tabla:
| [10, 15) | [15, 20) | [20, 25) | [25, 30) | [30, 35) | |
| fi | 3 | 5 | 7 | 4 | 2 |
Hallar:
1La moda, mediana y media.
2El rango, desviación media y varianza.
3Los cuartiles 1º y 3º.
4Los deciles 3º y 6º.
5Los percentiles 30 y 70.
17Dada la distribución estadística:
| [0, 5) | [5, 10) | [10, 15) | [15, 20) | [20, 25) | [25, ∞) | |
| fi | 3 | 5 | 7 | 8 | 2 | 6 |
Calcular:
Hallar:
1La mediana y moda.
2Cuartil 2º y 3º.
3Media.